Conditional Probability

Definition

The conditional probability of \(A\) given \(B\) is given by:

\[ P(A | B) = \frac{P(A \cap B)}{P(B)}.\]

It is important to note that the above is an abuse of notation, since \(A | B\) is not a set in the sigma-algebra to which the probability function can be applied. Hence \(P(A | B)\) should not be viewed as applying the function \(P\), but just special notation for the formally defined statement the probability of \(A\) given \(B\), or as a special function of two sets in the sigma algebra.

Intuition

This is a definition, and hence cannot be incorrect, however it is useful to justify why this definition is consistent with the idea of the probability of \(A\) occurring assuming that \(B\) has occurred.

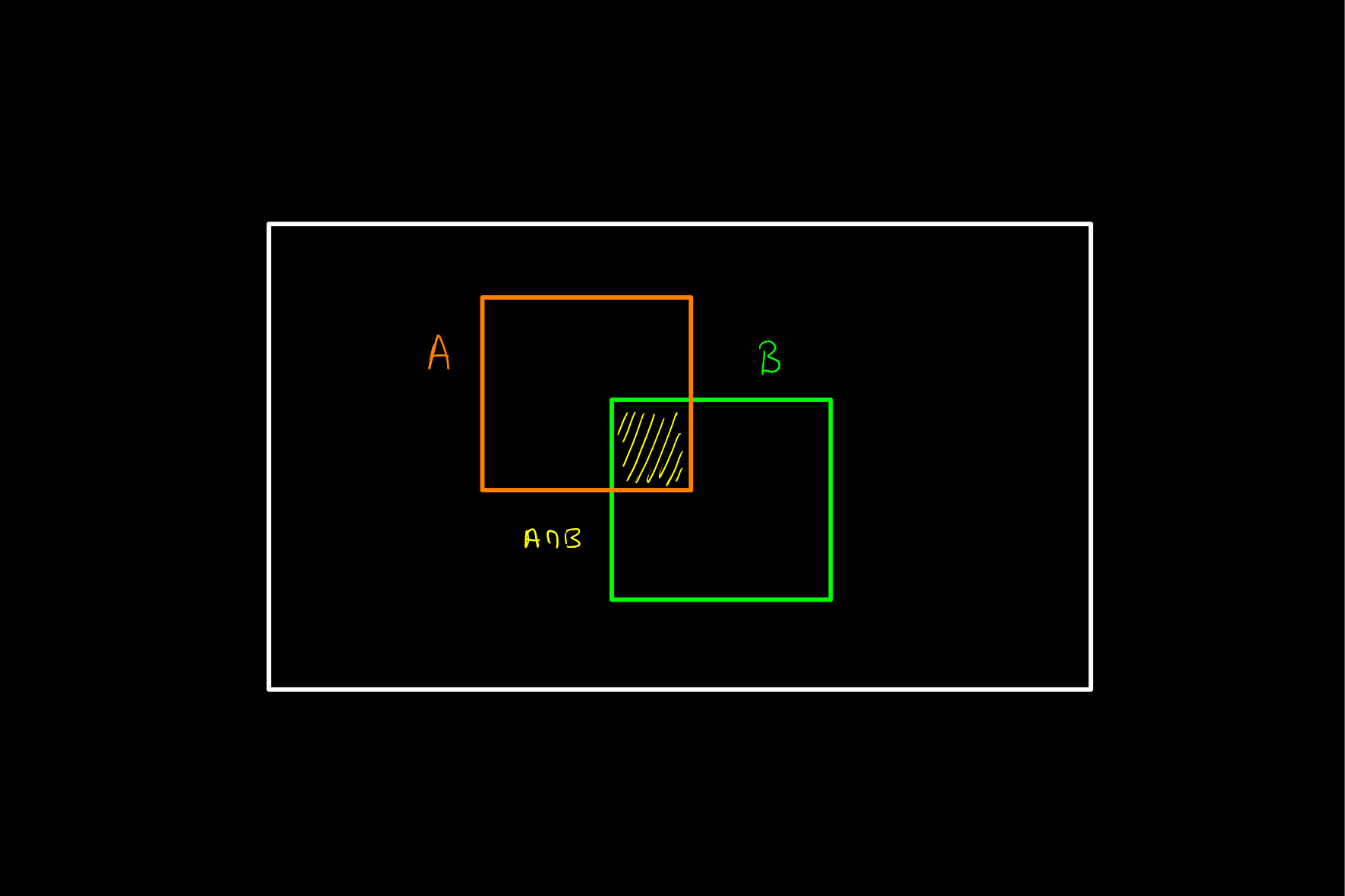
Consider for example a sample space \(\Omega\) with potentially overlapping events \(A\) and \(B\), where we wish to calculate the probability of \(A\) given \(B\).

Since we know \(B\) has occurred, we can use this information to restrict our sample space to \(B\) alone, this giving a better calculation for the probability of \(A\). The set of elements in the sigma algebra which are a subset of \(B\)

\[ \mathcal{F}' = \{X \in \mathcal{F} : X \subseteq B\}\]

is a \(\sigma\)-algebra on \(B\) using the same measure.

This \(\sigma\)-algebra contains only the events in which \(B\) has occurred (those that overlap with \(B\)).

Then, we could measure elements within this new sigma algebra with the same measure as the main probability space, however in order to make \(B\) itself a probability space we divide by the measure of the space \(B\). That is, we construct a new measure \(\mu_{B} : \mathcal{F}_B \to [0, 1]\) by:

\[ \mu_{B}(X) = \frac{\mu(X)}{\mu(B)}\]

from the original measure \(\mu\) on \(\Omega\).

This is a measure since we only multiply by a scaling factor.

This leaves one problem to resolve, being that \(A\) might not actually be in the sigma algebra \(\mathcal{F}_B\), as it may not be a subset of \(B\):

This is simple to resolve, by instead taking the measure of \(A \cap B\), since we are assuming \(B\) has occurred anyway, and \(A \cap B\) is measurable in the new measurable space \(B\).

This leaves our new probability formula:

\[ P(A \mid B) = \mu_B(A \cap B) = \frac{\mu(A \cap B)}{\mu(B)} = \frac{P(A \cap B)}{P(B)}.\]

Hence, intuitively, using the above diagram where probabilities are represented by areas, the probability of \(A\) given \(B\) is equal to the proportion of the area taken up by \(B\) which is also occupied by \(A\).

An important note to make is that often one may view \(A\) and \(B\) as events regarding different things, and hence consider them in different sample spaces. For example, one may consider the probability that someone is sick, and the probability that they have been coughing as being in two separate probability spaces. This is easily resolvable by considering the space to be the set of all states of both sickness and coughing. That is, in a simple case, if we previously had the sample spaces:

\[ \{\text{sick}, \text{not sick}\} \quad \text{and} \quad \{\text{coughing}, \text{not coughing}\}\]

both with the power set \(\sigma\)-algebra, then we can construct a new sample space using the Cartesian product, which happens to be the product measurable space if the events are independent (and otherwise is not).